Power systems form the backbone of modern society, driving industries, homes, and infrastructure. To grasp the intricacies of power systems, one must delve into the concept of power factor. But what is power factor, and why is it a critical parameter in electrical engineering? Let’s unravel this fundamental concept step by step.

What is Power Factor?

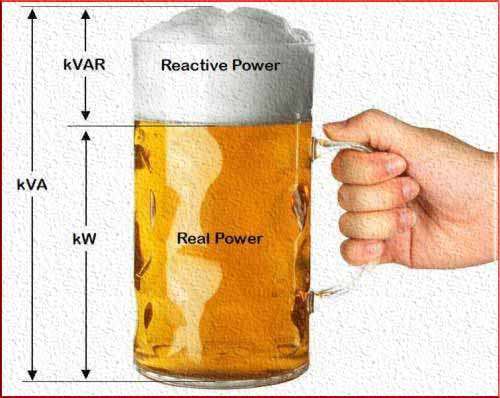
What is Power Factor? At its core, power factor is a measure of how effectively electrical power is being converted into useful work output. In other words, it quantifies the efficiency of power usage within an electrical system. To put it simply, power factor answers the question: “How much of the supplied power is actually being utilized for useful tasks?”

Importance of Power Factor

The importance of power factor becomes evident when considering the cost and efficiency aspects of electrical systems. Low power factor can result in increased energy consumption and utility bills. It can also lead to excessive heating in equipment and transmission lines, causing unnecessary wear and tear. Thus, understanding and optimizing power factor is crucial for reducing energy wastage and ensuring smooth operation of electrical systems.

Calculation of Power Factor

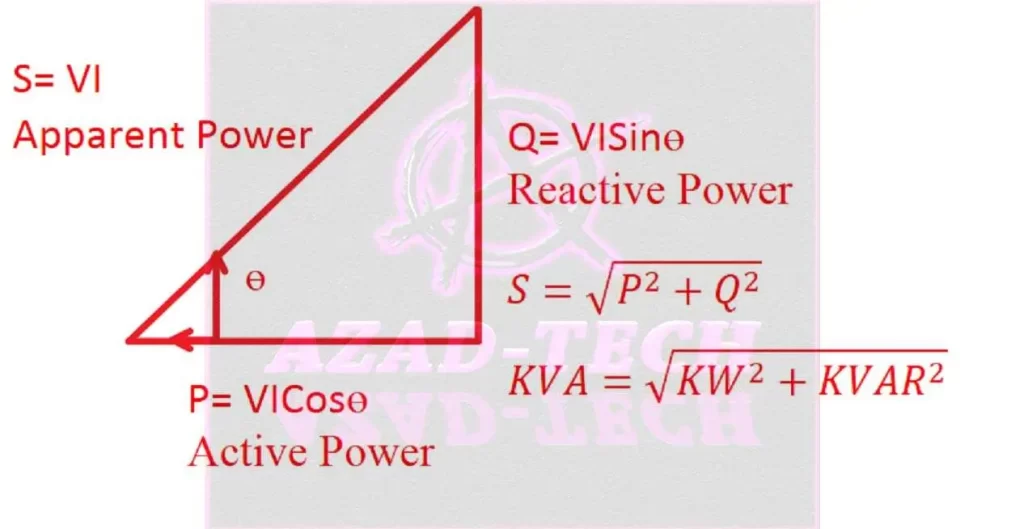
The power factor (PF) is mathematically expressed as the ratio of the real power (P, measured in watts) to the apparent power (S, measured in volt-amperes), where real power is the power actually consumed by resistive loads, and apparent power is the combination of real power and reactive power (Q, measured in volt-amperes reactive).

Power Factor (PF) = Real Power (P) / Apparent Power (S)

The Role of Reactive Power

Reactive power is where the keyword “what is power factor” comes into play yet again. It’s the power that oscillates between the source and the load due to the presence of inductive and capacitive elements. These elements are responsible for storing and releasing energy in the circuit.

Although they don’t directly perform useful work, they are essential for maintaining voltage levels and enabling the operation of inductive devices like motors and transformers.

Power Factor Correction

Now that we’ve established “what is power factor,” it’s time to discuss power factor correction. This process involves the use of capacitors and other devices to offset the effects of reactive power, thereby improving power factor. By doing so, utilities and industries can enhance energy efficiency, reduce losses, and optimize the use of electrical equipment.

The Cosine of Phase Angle

The power factor can also be expressed in terms of the cosine of the phase angle (θ) between the voltage and current waveforms. This relationship further elucidates the connection between the power factor and the alignment of these waveforms.

Power Factor (PF) = cos(θ)

Achieving Unity Power Factor: Ideally, power factor should be 1, known as unity power factor. This means that all the supplied power is used for useful work, and no reactive power is present. However, achieving unity power factor is often impractical due to the complex interplay of various electrical components.

What is Power Factor and How to Improve It?

Example 1: Power Factor Calculation

Let’s consider a factory that operates a set of machines with a total apparent power (S) of 500 kVA and a real power (P) of 400 kW. Using Equation 1 (Power Factor = P / S), we can calculate the power factor:

Power Factor (PF) = 400 kW / 500 kVA = 0.8

In this scenario, the power factor is 0.8, indicating that only 80% of the supplied power is being used for useful work, while the remaining 20% is lost as reactive power.

Example 2: Power Factor Improvement

Imagine a commercial building experiencing a power factor of 0.6 due to the presence of induction motors. This low power factor results in higher energy bills and potential penalties from the utility company. To improve the power factor, capacitors can be strategically installed.

Assuming the building has an apparent power (S) of 800 kVA and a real power (P) of 480 kW, we can calculate the current power factor.

Power Factor (PF) = 480 kW / 800 kVA = 0.6

To achieve a desired power factor of 0.9 (closer to unity), we can calculate the reactive power (Q) required to improve the power factor:

Desired Reactive Power (Q_desired) = S x sqrt(1 – PF^2)

Desired Reactive Power (Q_desired) = 800 kVA x sqrt(1 – 0.9^2)

Desired Reactive Power (Q_desired) = 400 kVAR

The additional reactive power needed is 400 kVAR. By installing capacitors with a total reactive power capacity of 400 kVAR, the power factor can be improved to 0.9, resulting in reduced energy consumption, lower utility bills, and improved system efficiency.

Example 3: Power Factor Improvement in an Industry

Consider an industrial plant with a power factor of 0.75. This plant operates a variety of machinery, including motors and transformers. The low power factor leads to increased energy costs and reduced efficiency. To address this issue, the plant decides to install power factor correction capacitors.

After installing the capacitors, the new apparent power (S_new) becomes 900 kVA, while the real power (P) remains at 600 kW. We can find the improved power factor:

Improved Power Factor (PF_new) = 600 kW / 900 kVA = 0.67

Although the power factor is improved, it hasn’t reached unity. The plant may decide to further optimize the power factor by adjusting the capacitor settings or implementing additional measures.

In these examples, we’ve explored how power factor calculation and improvement play a crucial role in managing energy efficiency, reducing costs, and maintaining the health of electrical systems. By understanding power factor and its implications, individuals and industries can make informed decisions to enhance their energy utilization practices.

Subscribe to our Newsletter “Electrical Insights Daily” to get the latest updates in Electrical Engineering. You can also Follow us LinkedIn and Facebook to see our latest posts on Electrical Engineering Topics.