Watts Law: Importance of Power Equation and Its Practical Applications
Discovering how electricity works can seem like a daunting task, especially when it comes to understanding complex equations like Watts Law. However, once demystified, this fundamental equation can shed light on the intricacies of power consumption and help you make informed decisions in various practical applications.
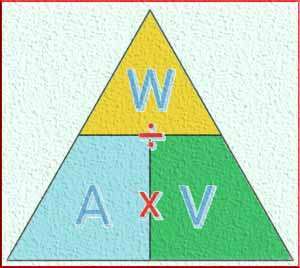
Table of Contents
In this article, we will break down the components of Watts Law and explain how it is relevant in everyday situations.
Watts Law, named after the physicist James Watt, relates three essential electrical variables: power (P), voltage (V), and current (I). By understanding how these variables are interconnected, you can calculate the amount of power consumed or produced in any electrical circuit. This knowledge is not only useful for professionals in the field, but also for everyday individuals who want to optimize their energy usage and make informed choices regarding appliances and electrical systems.
Understanding the Power Equation (P = IV)
The power equation, P = IV, is the foundation of Watts Law. It represents the relationship between power (P), current (I), and voltage (V) in an electrical circuit. Power, measured in watts, is the rate at which energy is transferred or consumed in a circuit. Current, measured in amperes, is the flow of electric charge through a conductor. Voltage, measured in volts, is the potential difference between two points in a circuit.
In simple terms, the power equation states that the power consumed or produced in a circuit is equal to the product of the current and voltage. This equation holds true for both DC (direct current) and AC (alternating current) circuits. Understanding this equation allows us to calculate the power consumed by an electrical device or determine the voltage and current required for a specific power output.
The three variables in Watts Law: Power (P), Current (I), and Voltage (V)
To fully grasp Watts Law, it is essential to understand the three variables involved: power (P), current (I), and voltage (V).
Power, as mentioned earlier, is the rate at which energy is transferred or consumed in a circuit. It is measured in watts and represents the amount of work done per unit time.
Current, on the other hand, refers to the flow of electric charge through a conductor. It is measured in amperes (A) and represents the amount of charge passing through a point in the circuit per unit time. Current can be direct (DC) or alternating (AC) depending on the nature of the circuit.
Voltage, also known as potential difference, is the electrical pressure that drives the current in a circuit. It is measured in volts (V) and represents the potential energy per unit charge. Voltage can be constant (DC) or vary with time (AC) depending on the type of circuit.
These three variables are interconnected through the power equation, allowing us to calculate and manipulate them to suit specific electrical requirements.
Practical applications of Watts Law in electronics
Watts Law finds practical applications in various fields, especially in electronics. Understanding this law enables engineers and technicians to design and optimize electrical systems, ensuring efficient power distribution and utilization. Here are a few practical applications of Watts Law in electronics:
1. Power Supply Design: Watts Law is essential in designing power supplies for electronic devices. By knowing the power requirements of a device and the desired voltage, engineers can calculate the current needed and design the power supply accordingly. This knowledge ensures that the power supply can deliver the required power without exceeding its limits.
2. Circuit Analysis: Watts Law is a fundamental tool in circuit analysis. By applying the power equation and manipulating the variables, engineers can analyze and predict the behavior of electrical circuits. This allows for troubleshooting and optimization of circuit designs.
3. Appliance Selection: Understanding Watts Law can help individuals make informed decisions when selecting appliances for their homes or businesses. By considering the power requirements of various appliances and the available voltage, individuals can choose appliances that are compatible with their electrical systems, ensuring optimal performance and energy efficiency.
4. Renewable Energy Systems: Watts Law is crucial in the design and implementation of renewable energy systems such as solar panels and wind turbines. By understanding the power requirements of the system and the available voltage, engineers can determine the number of panels or turbines needed and optimize the system’s output.
These are just a few examples of how Watts Law is applied in practical electronics. Its versatility and relevance make it an essential concept in the field of electrical engineering.
Calculating power using Watts Law
Calculating power using Watts Law is relatively straightforward once you understand the equation and have the necessary measurements. To calculate power, you need to know either the current and voltage or the resistance of the circuit.
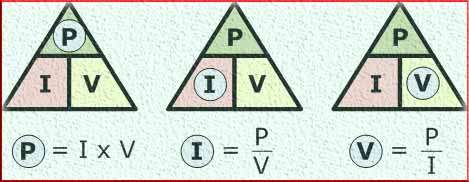
If you have the current (I) and voltage (V) measurements, you can simply multiply them together to obtain the power (P) in watts. This can be represented as P = IV.
If you have the resistance (R) of the circuit instead of the current, you can use Ohm’s Law (V = IR) to calculate the current.
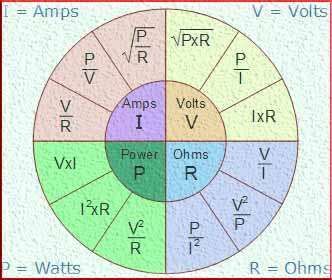
Once you have the current and voltage, you can again multiply them together to find the power.
It’s important to note that power calculations using Watts Law assume that the circuit is operating under ideal conditions and all components are linear. In real-world scenarios, factors such as resistance, capacitance, and inductance can affect the accuracy of the calculations.
the relationship between voltage, current, and power
The relationship between voltage, current, and power is essential to understand when applying Watts Law. This relationship can be summarized as follows:
Voltage and Current: Voltage and current have a direct relationship. An increase in voltage leads to an increase in current, given a fixed resistance. Similarly, a decrease in voltage leads to a decrease in current.
Voltage and Power: Voltage and power have a direct relationship, assuming a fixed resistance. An increase in voltage leads to an increase in power, while a decrease in voltage leads to a decrease in power.
Current and Power: Current and power have a direct relationship, assuming a fixed voltage. An increase in current leads to an increase in power, while a decrease in current leads to a decrease in power.
Understanding these relationships allows engineers and individuals to make informed decisions regarding power consumption, device selection, and electrical system optimization.
Examples of using Watts Law in real-world scenarios
To further illustrate the practical applications of Watts Law, let’s explore a few examples of using this equation in real-world scenarios:
1. Calculating Power Consumption: Suppose you have an appliance that operates at 120 volts and draws a current of 5 amperes. By applying Watts Law (P = IV), you can calculate the power consumed by the appliance as P = 120V 5A = 600 watts. This information allows you to estimate the energy consumption and cost of running the appliance.
2. Determining the Voltage Required: Let’s say you have an LED light that requires a power of 10 watts and operates at a current of 0.5 amperes. By rearranging the power equation (V = P/I), you can calculate the voltage required for the LED light as V = 10W / 0.5A = 20 volts. This information helps you select the appropriate power supply for the LED light.
3. Optimizing Solar Panel Output: Suppose you have a solar panel system with a voltage rating of 24 volts and a current rating of 10 amperes. By applying Watts Law, you can calculate the power output of the solar panel system as P = 24V 10A = 240 watts. This information allows you to optimize the system’s performance by adding or adjusting the number of panels to meet the desired power output.
These examples demonstrate how Watts Law can be applied in practical situations to make informed decisions and optimize energy usage.
Limitations and considerations when applying Watts Law
While Watts Law is a valuable tool in electrical engineering, it is essential to understand its limitations and consider factors that can affect its accuracy. Here are a few limitations and considerations when applying Watts Law:
1. Non-Linear Components: Watts Law assumes that all components in the circuit are linear, meaning their resistance or impedance remains constant regardless of the applied voltage or current. In reality, many components, such as diodes and transistors, exhibit non-linear behavior, which can affect the accuracy of power calculations.
2. Complex Circuits: Watts Law is most accurate when applied to simple circuits with a single power source and linear components. In complex circuits with multiple power sources and non-linear components, the accuracy of power calculations can be affected, and more advanced techniques may be required.
3. Power Factor: In AC circuits, the power factor represents the efficiency of power transfer from the source to the load. It takes into account the phase difference between voltage and current. When calculating power in AC circuits, it is important to consider the power factor to obtain accurate results.
4. Voltage Drop: In circuits with long wires or high resistance connections, voltage drop can occur, leading to a decrease in voltage at the load. When calculating power, it is crucial to consider the actual voltage at the load rather than the source voltage.
Understanding these limitations and considering the specific characteristics of the circuit or system being analyzed allows for more accurate power calculations and informed decision-making.
Common misconceptions and myths about Watts Law
Despite its importance and relevance, Watts Law is often misunderstood or subject to misconceptions. Let’s address some common misconceptions and myths about Watts Law:
1. Watts Law Only Applies to DC Circuits: This is a common misconception. Watts Law applies to both DC and AC circuits, as long as the components and measurements are consistent.
2. Power Equals Voltage: While voltage is an important component of power, power is a product of both voltage and current. Neglecting one or the other can lead to inaccurate power calculations.
3. Watts Law is Only for Electrical Engineers: While Watts Law is a fundamental concept in electrical engineering, it is relevant to anyone who uses electricity. Understanding this law empowers individuals to make informed decisions regarding power consumption and electrical devices.
4. Watts Law Accounts for Efficiency: Watts Law calculates the power consumed or produced in a circuit but does not take into account the efficiency of the system. Efficiency considerations, such as losses due to heat or resistance, must be addressed separately.
By dispelling these misconceptions, we can foster a better understanding of Watts Law and its practical applications.
In conclusion, Watts Law plays a crucial role in understanding and analyzing electrical circuits. By relating power, voltage, and current, this fundamental equation allows engineers and individuals to make informed decisions regarding power consumption, device selection, and system optimization.
Whether you are an electrical engineer designing complex circuits or an everyday individual looking to optimize energy usage, understanding Watts Law can provide valuable insights and empower you to make smarter choices in our modern world of electricity.
Worth Read Posts
- 14 Power Transformer Parts
- Transformers: Important Types
- Top 15 Power Transformer Manufacturers
- Transformer Electrical Interview
- 10 Transformer Tests Before Commissioning
- Transformer Oil Testing: 9 Important Tests
- Difference Between Demand Factor and Diversity Factor
- Demand Factor
- Fault Current Calculation: A Basic Overview
Follow Us on Social:
Subscribe our Newsletter on Electrical Insights to get the latest updates in Electrical Engineering.
#WattsLaw, #OhmsLaw, #ElectricalEngineering, #PowerFormula, #VoltageCurrentPower, #ElectricPower, #Wattage, #BasicElectronics, #PhysicsLaws, #EngineeringTips, #ElectricalFormulas, #STEMEducation, #ElectronicsBasics, #LearnElectricity, #CircuitDesign
