Derivation of Hysteresis Losses: Important Formulas
The derivation of the magnitude of hysteresis losses involves analyzing the energy dissipated during a complete cycle of magnetization and demagnetization of a ferromagnetic material.
Read More About
To simplify the derivation, we will consider a one-dimensional case where the material is magnetized along a single axis.
Hysteresis Losses Derivation
Let’s start by considering a small volume element of the ferromagnetic material, dV, with its magnetization, M, and the corresponding magnetic field intensity, H. The work done, dW, in magnetizing this small volume element is given by:
dW = H * dM
According to the magnetic hysteresis behavior, the relationship between M and H is nonlinear and can be represented by a hysteresis loop. To simplify the derivation, we will assume that the loop is symmetric with respect to the origin.
Now, the magnetization, M, is related to the magnetic field, B, through the magnetic permeability, μ, of the material:
B = μ * H
Taking the derivative of both sides with respect to H, we get:
dB = μ * dH
Since the loop is symmetric, the area enclosed by the loop is proportional to the energy dissipated during one complete cycle. Let’s denote this area as A.
Now, the work done in magnetizing the small volume element is equal to the change in magnetic energy, dU, within that element:
dU = B * dB * dV
Substituting the expressions for B and dB, we have:
dU = μ * H * μ * dH * dV = μ^2 * H * dH * dV
Integrating both sides over the volume of the material, V, we obtain the total magnetic energy, U, dissipated during one complete cycle:
U = ∫(μ^2 * H * dH * dV)
Now, using the fact that B = μ * H, we can express the magnetic energy in terms of B:
U = ∫(B * dB * dV)
The hysteresis losses, P_h, per unit volume can be defined as the energy dissipated per unit volume:
P_h = U / V
Substituting the expression for U, we have:
P_h = (1 / V) * ∫(B * dB * dV)
Since the integral represents the area enclosed by the hysteresis loop, denoted as A, we can rewrite the expression for these losses as:
P_h = A / V
Therefore, the magnitude of hysteresis losses per unit volume is given by the area enclosed by the hysteresis loop divided by the volume of the material.
It’s important to note that the derivation presented here provides a conceptual understanding of the hysteresis losses magnitude. In practice, more detailed calculations may involve additional considerations, such as the specific shape of the hysteresis loop and the material’s hysteresis characteristics.
What are hysteresis losses?
Hysteresis losses refer to the energy dissipated as heat when a magnetic material undergoes a reversal of magnetization due to alternating magnetic fields. This loss occurs because of the lag or hysteresis effect in the material’s magnetization and demagnetization.
What causes hysteresis losses in magnetic materials?
Hysteresis losses occur due to the inherent property of magnetic materials to retain some magnetization even after the magnetic field causing it has been removed. When the field changes direction, the material’s magnetization has to realign, leading to energy losses.
How are hysteresis losses calculated?
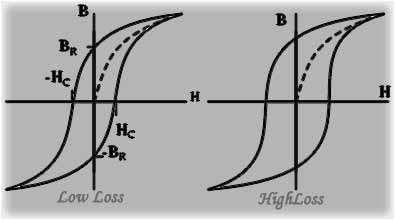
Hysteresis losses are quantified by the area enclosed by the hysteresis loop on the B-H (magnetic flux density vs. magnetic field strength) curve of the material. The energy dissipated per cycle is proportional to this loop’s area.
Which factors influence hysteresis losses in magnetic materials?
Factors affecting these losses include the material’s magnetic properties, such as coercivity (resistance to demagnetization), saturation magnetization, and frequency and amplitude of the alternating magnetic field applied.
What are some common applications where hysteresis losses are important?
Hysteresis losses are crucial in power transformers, electric motors, inductors, and any device where magnetic materials are used for their magnetic properties. Minimizing these losses is essential for improving efficiency in these applications.
How can hysteresis losses be reduced?
Using materials with lower hysteresis loop areas, such as certain types of soft magnetic materials, or employing materials with lower coercivity, can help reduce these losses. Additionally, operating at lower frequencies can mitigate these losses.
Are hysteresis losses a significant concern in electrical devices?
These losses can be significant, especially in devices handling high frequencies or in those where energy efficiency is crucial. Minimizing these losses is important for improving the overall efficiency and performance of electrical devices.
Can hysteresis losses be completely eliminated?
While it’s impossible to entirely eliminate these losses in magnetic materials, advancements in material science and engineering allow for the use of materials with reduced hysteresis effects, helping to minimize these losses.
How do hysteresis losses affect the efficiency of electrical devices?
These losses result in the conversion of electrical energy into heat, reducing the overall efficiency of devices that rely on magnetic materials. This loss manifests as heat, affecting performance and potentially requiring additional cooling mechanisms.
Are hysteresis losses more significant in specific types of materials?
Yes, different magnetic materials exhibit varying levels of these losses. Soft magnetic materials, like iron-silicon alloys, have lower losses compared to hard magnetic materials, such as certain ferrites.
Can hysteresis losses change with the operating conditions of a device?
Yes, the magnitude of hysteresis losses can vary with factors like temperature, frequency, and the magnetic properties of the material. Higher frequencies and temperatures can increase these losses.
Are there design techniques to mitigate hysteresis losses in devices?
Yes, optimizing the design of magnetic circuits by using materials with lower hysteresis, employing laminated cores to reduce eddy current losses, and utilizing design approaches that minimize the magnetic field changes can help mitigate these losses.
How do hysteresis losses impact the lifespan of electrical devices?
Excessive hysteresis losses can lead to increased heat generation within the device, potentially shortening its lifespan due to thermal stress on components.
Are there standards or regulations that address hysteresis losses in electrical devices?
Various industry standards and regulations focus on energy efficiency in electrical devices, indirectly influencing the consideration and reduction of these losses to improve overall efficiency.
Can modeling and simulation be used to predict and minimize hysteresis losses?
Yes, computer simulations and modeling can predict these losses in magnetic materials and aid in the design process to optimize device performance and reduce losses.
Worth Read Posts
Follow us on LinkedIn”Electrical Insights” to get the latest updates in Electrical Engineering. You can also Follow us on LinkedIn and Facebook to see our latest posts on Electrical Engineering Topics.
