Work Function Formula:

The work function (φ) represents the minimum energy required to eject electrons from a metal surface in the photoelectric effect. The work function formula can be expressed through three related equations:

1. E(light) = φ + KE

• Where E(light) is the total energy of incident light
• φ is the work function
• KE is the kinetic energy of ejected electrons

2. φ = hf

• Where h is Planck’s constant
• f is the frequency of radiation

3. φ = hc/λ

• Where h is Planck’s constant
• c is the speed of light
• λ is the wavelength

The choice of the equation for the work function formula depends on the given variables in the problem. Any excess energy above the work function is converted into the kinetic energy of the ejected electrons.

What is Work Function?

In classical physics, the concept of work function is not explicitly defined. The term “work function” is primarily used in the context of quantum mechanics and the behavior of electrons at the atomic and subatomic level.

In classical physics, the concept of work is defined as the transfer of energy that occurs when a force acts on an object and causes it to move a certain distance. The work done on an object is given by the equation:

Work = Force × Distance × cos(θ)

where the force is applied in the direction of the displacement, and θ is the angle between the force and the direction of displacement.

Classical physics does not specifically address the minimum energy required to remove electrons from a material or the quantization of energy levels associated with electronic transitions. These aspects are better described by quantum mechanics, where the work function plays a crucial role in understanding the behavior of electrons in materials, particularly in phenomena such as the photoelectric effect and electron emission.

Therefore, the concept of work function is primarily a quantum mechanical concept and does not have a direct counterpart in classical physics.

Work Function in Quantum Physics

In quantum physics, the work function refers to the minimum amount of energy required to remove an electron from a material and move it to a point just outside the material’s surface. It is a fundamental concept that helps describe the behavior of electrons in materials and is particularly relevant in the study of the photoelectric effect and electronic properties.

According to quantum mechanics, electrons in a material are described by discrete energy levels. The work function represents the energy difference between the highest occupied energy level of electrons within the material (known as the Fermi level) and the energy level of electrons just outside the material. When the energy of incident photons or particles exceeds the work function, electrons can be emitted from the material’s surface through a process called photoemission.

The work function is typically denoted by the symbol Φ and is measured in electron volts (eV) or joules (J). It depends on the specific material and its electronic structure, including factors such as the type of material, crystal structure, temperature, and surface conditions.

The work function can be experimentally determined by measuring the energy of incident photons required to initiate photoemission from a material’s surface. It is an important parameter in understanding the interaction between light and matter, as well as in the design and optimization of devices such as solar cells, photodetectors, and electron emission sources.

Light, as Sir Albert Einstein proposed, manifests as a multitude of discrete energy packets known as photons. Each photon carries an energy denoted by hf, where h represents Planck’s constant and f corresponds to the frequency of the light.

When light impinges upon a metal surface, electrons residing on the surface absorb energy from the light and subsequently become emitted from the surface—an occurrence referred to as photoemission in classical terms.

Since the energy of a single photon, Ephoton, equals hf, the energy of each photon relies solely on the frequency of the light. Thus, the frequency constitutes the sole variable determining the energy of the photon. Significantly, it has been observed that no photoemission occurs from a metal surface unless the frequency of the incident light surpasses a certain threshold. Consequently, a minimum frequency of the incident light is necessary to initiate photoemission.

In cases where the frequency of light exceeds this aforementioned minimum frequency, any additional energy carried by the photon becomes converted into kinetic energy of the emitted electron. Hence, the velocity at which the electron is liberated from the metal surface hinges upon the frequency of the incident light, rather than its intensity (or brightness).

However, in situations where the intensity of the incident light amplifies while its frequency remains unaltered, the number of photons impinging on the metal surface escalates. Consequently, a greater quantity of emitted electrons is generated, though the kinetic energy of each electron remains unaltered, owing to the fixed frequency of the incident light.

Threshold Frequency, a pivotal notion in this context, delineates the frequency of incident light beneath which no photoemission originates from a metal surface. The absence of kinetic energy in the electrons characterizes frequencies below this threshold frequency, underscoring its significance.

Each metal possesses its own distinct threshold frequency, highlighting the divergent values this critical frequency assumes across various metallic materials.

Work Function Formula derivation

The work (Φ) function formula can be derived by considering the conservation of energy in the process of photoemission. Let’s go through the derivation step by step:

Start with the energy of a photon: E = hν Here, E represents the energy of a photon, h is Planck’s constant, and ν is the frequency of the incident light.

Assume that the photon transfers its entire energy to an electron during the photoemission process. Therefore, the energy of the electron can be equated to the energy of the incident photon: E_electron = E

The energy of the electron can be divided into two parts: the kinetic energy (E_k) and the work function energy (Φ).

Thus, we can write: E_electron = E_k + Φ

Equating E and E_electron, we have: E = E_k + Φ

Substituting the value of E from step 1, we get: hν = E_k + Φ

Rearranging the equation, we obtain the work (Φ) function formula: Φ = hν – E_k

This derivation shows that the function (Φ) is equal to the difference between the energy of the incident photon (hν) and the maximum kinetic energy of the emitted electron (E_k). It demonstrates the energy conservation principle in photoemission and provides a quantitative relationship between these variables.

What is the Symbol of Threshold Frequency

The symbol of threshold frequency is typically represented by f0​ or ν0​ in physics. Threshold frequency refers to the minimum frequency of incident light that can cause the emission of electrons from a material’s surface, based on the photoelectric effect. Below this frequency, no matter how intense the light is, electrons will not be ejected.

The threshold frequency is directly related to the work function of the material, which is the minimum energy required to release an electron. In simpler terms, the light must have enough energy (corresponding to its frequency) to overcome the material’s work function for the photoelectric effect to occur.

The relationship between threshold frequency and work function is given by the formula:

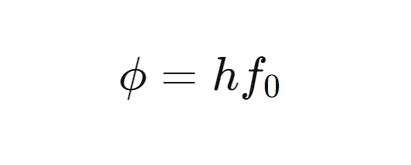
Where:

• ϕ\phiϕ is the work function of the material (in joules or electron volts),
• hhh is Planck’s constant (6.626×10−34 J.s
• f0 is the threshold frequency (in Hz).

The formula shows that the work function is proportional to the threshold frequency, implying that different materials will have different threshold frequencies based on their work functions.

Work Function Formula

The work function (Φ) of a material can be expressed using the following formula:

Φ = hν – E_k

where:

• Φ represents the work function,
• h is Planck’s constant (approximately 6.626 x 10^-34 J·s),
• ν denotes the frequency of the incident light or radiation,
• E_k represents the maximum kinetic energy of the emitted electrons.

In this formula, hν corresponds to the energy of the incident photons, which is determined by the frequency of the light (ν). The term E_k represents the maximum kinetic energy of the emitted electrons, which depends on the energy of the incident photons and the characteristics of the material’s surface.

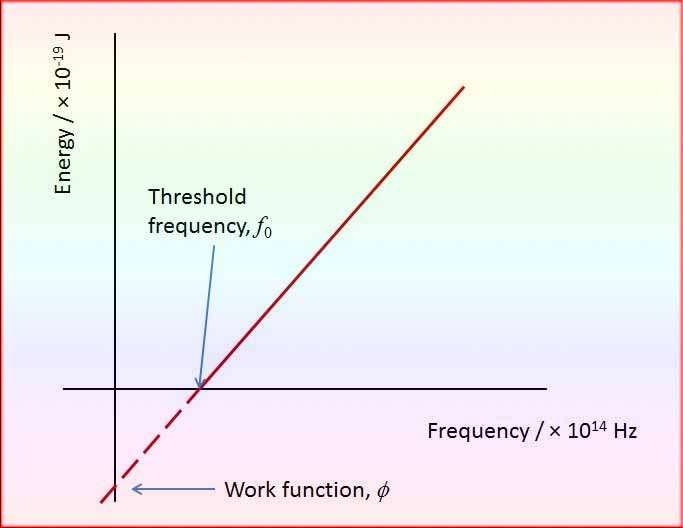
By subtracting the maximum kinetic energy (E_k) from the energy of the incident photons (hν), the work function (Φ) is obtained. The Φ function represents the minimum amount of energy required to remove an electron from the material and release it outside the surface.

Work Function and Threshold Frequency

Here’s a table of the Φ and threshold frequency of various metals, along with their corresponding values in electron volts (eV):

Metals	Threshold Frequency (Hz)	Work Function (eV)
Aluminum	7.30 x 10^14	4.08
Copper	8.95 x 10^14	4.65
Gold	6.68 x 10^14	5.10
Silver	9.03 x 10^14	4.73
Platinum	8.34 x 10^14	5.65
Iron	6.71 x 10^14	4.50
Zinc	6.73 x 10^14	4.30
Titanium	6.98 x 10^14	4.33
Nickel	8.62 x 10^14	5.01
Tungsten	6.17 x 10^14	4.55
Chromium	7.48 x 10^14	4.50
Palladium	8.54 x 10^14	5.12
Molybdenum	5.85 x 10^14	4.40
Rhodium	7.96 x 10^14	5.59
Ruthenium	8.51 x 10^14	4.69
Iridium	8.06 x 10^14	5.16
Lead	7.40 x 10^14	4.50
Beryllium	5.03 x 10^14	3.95
Sodium	4.74 x 10^14	2.28
Potassium	4.83 x 10^14	2.30
Magnesium	6.57 x 10^14	3.68
Lithium	5.14 x 10^14	2.91
Cesium	4.74 x 10^14	2.14
Rubidium	4.91 x 10^14	2.09
Barium	4.70 x 10^14	2.70

Please note that the values provided are approximate and can vary depending on factors such as crystal structure, surface conditions, and impurities.

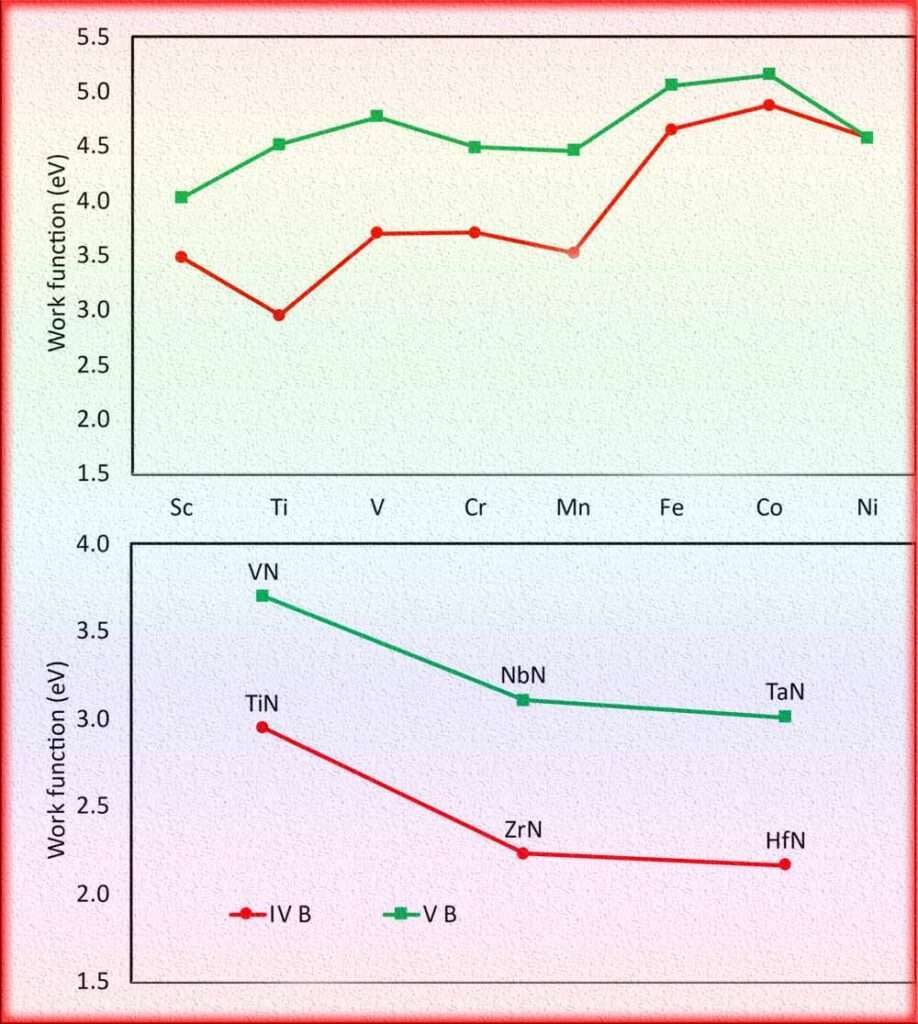
work function photoelectric effect

The work function plays a significant role in the photoelectric effect, which is the phenomenon where electrons are emitted from a material’s surface when it is exposed to light or other forms of electromagnetic radiation. The work (Φ) function represents the minimum energy required to remove an electron from the material and release it outside the surface.

In the context of the photoelectric effect, the Φ can be explained using the following key points:

Threshold Frequency: Each material has a specific threshold frequency, denoted as ν₀, which corresponds to the minimum frequency of incident light required to initiate the photoelectric effect. The threshold frequency is related to the work function as follows:

ν₀ = (Φ / h)

Here, h is Planck’s constant, and Φ represents the work function.

Emission of Electrons: When the frequency of incident light exceeds the threshold frequency (ν > ν₀), electrons can be emitted from the material’s surface. The energy of each photon (E) is given by:

E = hν

If the energy of an incident photon is greater than or equal to the work function (E ≥ Φ), the excess energy beyond the Φ is converted into the kinetic energy of the emitted electron.

Kinetic Energy of Electron = E – Φ

Intensity vs. Kinetic Energy: The intensity or brightness of the incident light affects the number of photons striking the surface per unit time, leading to a greater number of emitted electrons. However, the intensity does not directly impact the kinetic energy of the emitted electrons. The kinetic energy depends solely on the frequency (energy) of the incident photons and the Φ function.

You May Also Want to Know about

Polarization Index

Motor Service Factor 

Stopping Potential: The stopping potential in a photoelectric experiment refers to the minimum potential difference required to halt the emitted electrons from reaching a collecting electrode. The stopping potential is directly related to the maximum kinetic energy of the emitted electrons and can be measured experimentally to determine the relationship between frequency and kinetic energy.

The Φ determines the threshold frequency required for the photoelectric effect and represents the minimum energy needed to liberate an electron from a material. The energy of incident photons exceeding the function leads to the emission of electrons, with the excess energy contributing to their kinetic energy. The work function and the frequency of incident light are fundamental factors influencing the photoelectric effect.

Conclusion

In conclusion, the work function is a fundamental concept in physics that relates to the photoelectric effect and the emission of electrons from a material’s surface when exposed to light or other forms of electromagnetic radiation. Here are the key points to remember about the Φ function:

Definition: The work function represents the minimum energy required to remove an electron from a material and release it outside the surface. It is specific to each material and is typically denoted by the symbol Φ.

Energy Conservation: In the photoelectric effect, the energy of incident photons (E = hν) is used to overcome the Φ function and provide kinetic energy to emitted electrons.

Threshold Frequency: Each material has a threshold frequency (ν₀), which corresponds to the minimum frequency of light required to initiate the photoelectric effect. The threshold frequency is related to the work through the equation ν₀ = Φ/h.

Photoemission: When the frequency of incident light exceeds the threshold frequency, electrons can be emitted from the material’s surface. The excess energy of the photons beyond the work function is converted into the kinetic energy of the emitted electrons.

Independence from Intensity: The work function and the kinetic energy of the emitted electrons are determined solely by the frequency (energy) of the incident photons. The intensity (brightness) of the light affects the number of photons but does not directly influence the kinetic energy of the electrons.

Application: The understanding of the work function is crucial in various areas, such as solar energy conversion, photodetectors, and the design of electronic devices based on the photoelectric effect.

By considering the work function, scientists and engineers can analyze and predict the behavior of materials and optimize their performance in various applications that involve the interaction of light and matter.

Follow us on LinkedIn“Electrical Insights” to get the latest updates in Electrical Engineering. You can also Follow us LinkedIn to see our latest posts.

Frequently Asked Questions