Two 150 kVA single phase transformers are connected in parallel
Problem:
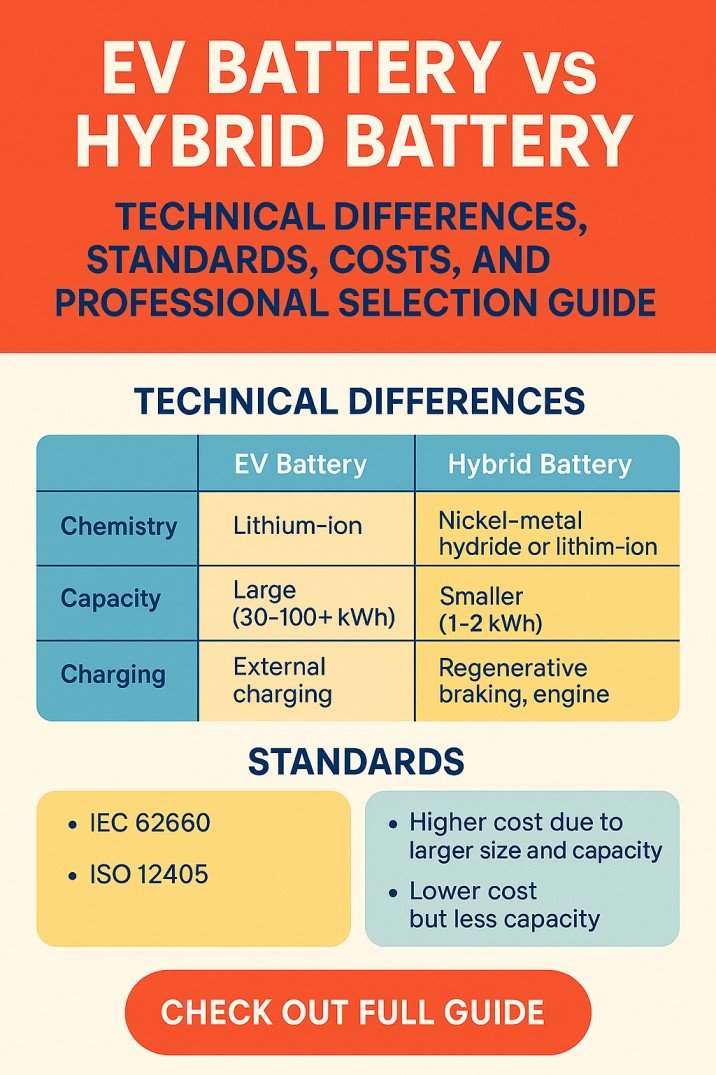
Two 150 kVA single-phase transformers are connected in parallel on both the primary and secondary sides. The first transformer has an ohmic drop of 0.6% at full load and an inductive drop of 7% at full load current. The second transformer has an ohmic drop of 0.8% and an inductive drop of 3%. Calculate how they will share a load of 250 kVA at 0.85 power factor lagging.
Solution:
Let’s solve this new problem step by step:
First, let’s define the parameters for each transformer: Transformer 1 (T1):
- Rated power: 150 kVA
- Ohmic drop: 0.6%
- Inductive drop: 7%
- Transformer 2 (T2):
- Rated power: 150 kVA
- Ohmic drop: 0.8%
- Inductive drop: 3%
Calculate the impedance of each transformer:
T1: Z1 = R1 + jX1 = 0.6% + j7%
= 0.006 + j0.07 pu
T2: Z2 = R2 + jX2 = 0.8% + j3%
= 0.008 + j0.03 pu
Express the load in per unit (pu) based on the total rated power of the transformers:
Base power = 150 kVA + 150 kVA = 300 kVA Load in pu
= 250 kVA / 300 kVA = 0.8333 pu
The current sharing between the transformers will be inversely proportional to their impedances:
I1 = I * (Z2 / (Z1 + Z2)) I2
= I * (Z1 / (Z1 + Z2)) Where I is the total load current.
Calculate the magnitudes of the impedances:
|Z1| = √(0.006² + 0.07²) = 0.0703 pu |Z2|
= √(0.008² + 0.03²) = 0.0310 pu
Calculate the current sharing:
I1 = 0.8333 * (0.0310 / (0.0703 + 0.0310)) = 0.2584 pu
I2 = 0.8333 * (0.0703 / (0.0703 + 0.0310)) = 0.5749 pu
To get the actual power sharing, multiply these currents by the base power and the power factor: S1 = 0.2584 * 300 kVA
= 77.52 kVA P1
= 77.52 kVA * 0.85 = 65.89 kW
Q1 = 77.52 kVA * sin(acos(0.85)) = 41.09 kVAr
S2 = 0.5749 * 300 kVA = 172.47 kVA
P2 = 172.47 kVA * 0.85 = 146.60 kW
Q2 = 172.47 kVA * sin(acos(0.85)) = 91.42 kVAr
Therefore, the load sharing will be:
Transformer 1 will carry approximately 77.52 kVA (65.89 kW and 41.09 kVAr)
Transformer 2 will carry approximately 172.47 kVA (146.60 kW and 91.42 kVAr)
This uneven distribution is due to the difference in their impedances. Transformer 2, with its lower overall impedance, carries the majority of the load.
The total load is indeed 250 kVA (77.52 + 172.47), with a total active power of 212.49 kW (65.89 + 146.60) and reactive power of 132.51 kVAr (41.09 + 91.42), which corresponds to the 0.85 power factor lagging.
Worth Read Posts
- Power Transformer Testing
- Power Transformer Parts
- Hysteresis Loss and Eddy Current Loss
- Derivation of Hysteresis Losses
- Transformers: Important Types, Features & Components
- Transformer Tests Before Commissioning
- Transformer Electrical Interview
Follow us on LinkedIn, “Electrical Insights,” to get the latest updates on electrical engineering.