Period and Frequency: A Comprehensive Analysis
Table of Contents
Introduction
Understanding the fundamental concepts of period and frequency is essential in various fields, including physics, engineering, and mathematics. Period and frequency are interconnected quantities that describe the behavior of waveforms and oscillations. In this article, we delve into the intricacies of the period vs frequency relationship, unraveling their definitions, calculations, and significance. Join us as we explore the fundamental nature of these concepts and shed light on their applications in different domains.
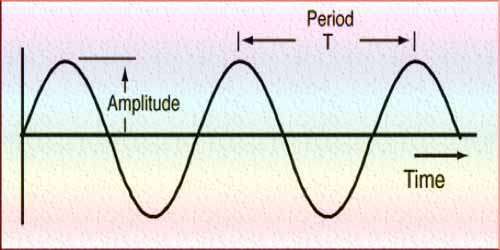
Defining Period and Frequency
Period and frequency are reciprocal quantities that convey information about the timing and repetition of events within a given timeframe. Period (T) represents the time it takes for a complete cycle of a periodic waveform to occur. It is typically measured in seconds (s) or any applicable time unit. Frequency (f) measures the number of cycles completed per unit of time and is expressed in hertz (Hz) or an appropriate frequency unit.
Mathematical Relationship
Frequency and Period share an inverse relationship. Mathematically, this relationship is expressed as follows:
f = 1/T
where f represents frequency and T represents the period. This equation signifies that frequency is the reciprocal of the period, and vice versa. Consequently, as the period increases, the frequency decreases, and vice versa.
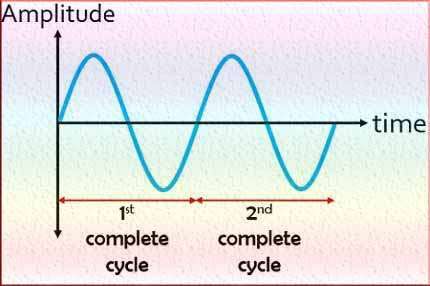
Calculating Period from Frequency
To calculate the period from the frequency, use the formula:
T = 1/f
Conversely, to derive the frequency from the period, apply the equation:
f = 1/T
These equations provide a straightforward approach to converting between period and frequency, enabling precise measurements and analysis in numerous applications.
Example of pendulum
Suppose you have a pendulum that swings back and forth, and you want to determine its period and frequency. You observe that the pendulum completes 10 swings in 20 seconds.
Calculating Frequency: To find the frequency, you can use the formula:
f = 1 / T
Given that the period (T) is the time it takes for one complete swing of the pendulum, you can calculate the frequency (f) as follows:
f = 1 / 20 seconds f = 0.05 Hz
Therefore, the frequency of the pendulum’s swings is 0.05 Hz, indicating that it completes 0.05 cycles (or swings) per second.
Calculating Period
To determine the period, you can use the formula:
T = 1 / f
Using the previously calculated frequency (f) of 0.05 Hz, you can calculate the period (T) as follows:
T = 1 / 0.05 Hz T = 20 seconds
Hence, the period of the pendulum’s swings is 20 seconds, indicating that it takes 20 seconds to complete one full swing.
In this example, we used the formulas for Frequency and Period to calculate the values based on the given information. The frequency was determined to be 0.05 Hz, representing 0.05 swings per second, while the period was found to be 20 seconds, indicating that it takes 20 seconds for one complete swing. These calculations demonstrate how the reciprocal relationship between period and frequency can be utilized to analyze and quantify the behavior of oscillatory systems like the pendulum.
Remember to ensure consistency in units when applying these formulas to obtain accurate results.
Significance of Period and Frequency
The period and frequency of a waveform carry significant implications across various disciplines:
Physics and Engineering: In physics and engineering, understanding the relationship between period and frequency is crucial for analyzing and manipulating signals, waves, and oscillatory systems. This knowledge is vital in areas such as signal processing, communication systems, electronics, and acoustics.
Harmonic Analysis: Period and frequency play a central role in harmonic analysis, where complex waveforms are decomposed into their constituent sinusoidal components. By determining the periods and frequencies of these harmonics, researchers can gain insights into the structure and behavior of signals and systems.
Music and Sound: Period and frequency are fundamental to the study of music and sound. Musicians and audio engineers utilize these concepts to tune instruments, analyze harmonics, and achieve specific tonal characteristics. Understanding the relationship between period and frequency is crucial for achieving accurate pitch and maintaining musical harmony.
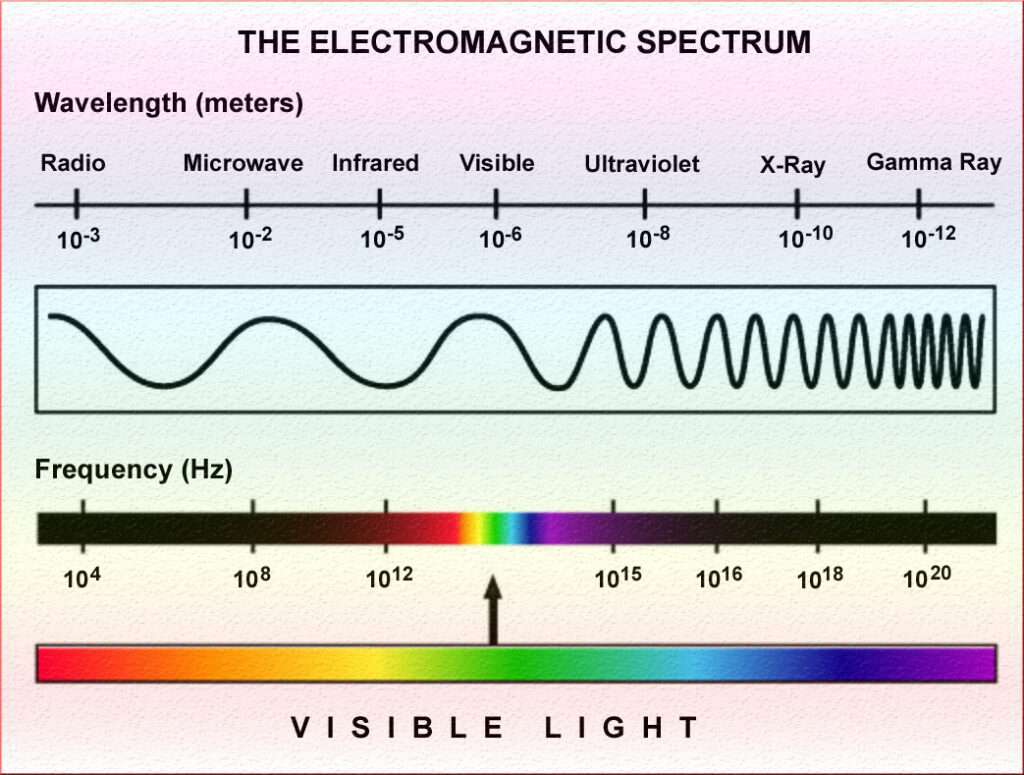
Optics and Electromagnetic Waves: In optics and the study of electromagnetic waves, the period and frequency of light waves are crucial. These properties determine the color and intensity of light, as well as phenomena like interference and diffraction. Period and frequency calculations are used to design optical devices, analyze spectra, and understand the behavior of electromagnetic radiation.
Conclusion
Period and frequency represent vital concepts in various scientific, engineering, and mathematical fields. They provide a quantitative understanding of waveforms, oscillations, and repetitive phenomena. The reciprocal relationship between period and frequency is governed by precise mathematical equations, enabling seamless conversions and accurate measurements.
By grasping the significance of period and frequency, researchers, engineers, and enthusiasts can delve deeper into the intricacies of their respective domains, driving innovation and advancing our understanding of the natural world.
Follow us on LinkedIn“Electrical Insights” to get the latest updates in Electrical Engineering. You can also Follow us LinkedIn to see our latest posts.
Frequently asked questions
What is the definition of period in physics?
In physics, period refers to the time it takes for a complete cycle of a repetitive event or motion to occur.
How is the period of a wave calculated?
The period of a wave is calculated by taking the reciprocal of its frequency. Mathematically, it is expressed as T = 1/f, where T represents the period and f represents the frequency.
What is the relationship between period and frequency?
The relationship between period and frequency is inverse. As the frequency of a wave increases, its period decreases, and vice versa. Mathematically, the relationship can be expressed as T = 1/f or f = 1/T.
Can you explain the concept of frequency in simple terms?
Frequency is a measure of how many cycles or oscillations occur in a given unit of time. It represents the number of complete cycles of a wave that occur in one second and is commonly measured in Hertz (Hz).
How do you convert between period and frequency?
To convert between period and frequency, you can use the formula T = 1/f for converting from frequency to period, and f = 1/T for converting from period to frequency. Simply substitute the known value into the formula to obtain the desired conversion.
What are the units of period and frequency?
The unit of period is typically expressed in seconds (s), while the unit of frequency is Hertz (Hz), which represents cycles per second.
What are some real-life examples where understanding period and frequency is important?
Understanding period & frequency is important in various fields, such as music, telecommunications, and physics. For example, musicians need to understand the period and frequency of musical notes to create harmonious melodies. In telecommunications, the understanding of frequency and period is crucial for transmitting and receiving signals. In physics, period and frequency play a vital role in analyzing and studying waves, vibrations, and oscillatory phenomena.
